未分類

分類されていない話題

モザイク

知り合いからのリクエスト。「モザイク」より「ノイズ」と表現したほうが近いか。

繰り返しのないランダムな白黒の点ということだったので、円周率から作成。
ファイル形式は指定どおり24bitBMP。解像度 960x540

画像をクリック ⇒ 移動先で右クリック ⇒ 名前をつけて画像を保存または
右クリック ⇒ 名前をつけてリンク先を保存からどうぞ。

２色

明度 : 0,255

４色

明度 : 0,85,170,255

2011/ 2/14

Windows小技

ショートカットに相対リンクを使う

USBフラッシュメモリに作ったリンクがドライブレターが変わっても使えるようにする方法
動作確認ＯＳ：Windows XP Professional
まず普通にショートカットを作り(対象をドラッグしながらAltキーを押してドロップすると楽チン)
作ったショートカットを右クリックして「プロパティ」を開き、作業フォルダの欄を空白にする。
この後の操作は対象がファイルかフォルダかで異なる。

作成したのがファイルの場合
リンク先を

\RunDLL32.exe Shell32.dll,ShellExec_RunDLL "相対パス"

とする

作成したのがフォルダの場合
リンク先を

%windir%\explorer.exe /n,"相対パス"

とする

原理に関しては長くなるので割...正直に言うと時間が経ちすぎて覚えていない。
こうならないための覚え書きなのに。
この通りにやったのにうまくいかない、他のＯＳでもできたなどの情報がありましたら連絡いただけるとありがたいです。

三角関数の合成

一般的な三角関数ａsin(ωt + θ)の和についてまとめ(たい。いつか。)

うなりの発生(ａが等しい場合)

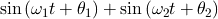
$\sin{(\omega_1 t + \theta_1)} + \sin{(\omega_2 t + \theta_2)}$

を変形する

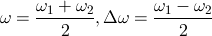
$\omega = \frac{\omega_1 + \omega_2}{2},\Delta\omega = \frac{\omega_1 - \omega_2}{2}$ $\theta = \frac{\theta_1 + \theta_2}{2},\Delta\theta = \frac{\theta_1 - \theta_2}{2}$

とおき

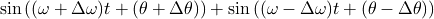
$\sin{((\omega + \Delta\omega) t + (\theta + \Delta\theta))} + \sin{((\omega - \Delta\omega) t + (\theta - \Delta\theta))}$

にEulerの公式を適用して

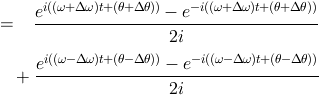
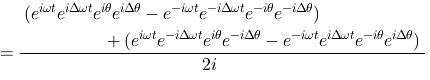
$\frac{e^{i((\omega + \Delta\omega) t + (\theta + \Delta\theta))} - e^{-i((\omega + \Delta\omega) t + (\theta + \Delta\theta))}}{2i} + \frac{e^{i((\omega - \Delta\omega) t + (\theta - \Delta\theta))} - e^{-i((\omega - \Delta\omega) t + (\theta - \Delta\theta))}}{2i}$ $= \frac{(e^{i \omega t}e^{i \Delta\omega t}e^{i \theta}e^{i \Delta\theta}-e^{-i \omega t}e^{-i \Delta\omega t}e^{-i \theta}e^{-i \Delta\theta}) +(e^{i \omega t}e^{-i \Delta\omega t}e^{i \theta}e^{-i \Delta\theta}-e^{-i \omega t}e^{i \Delta\omega t}e^{-i \theta}e^{i \Delta\theta})}{2i}$ $= 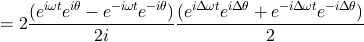2\frac{(e^{i \omega t}e^{i \theta} - e^{-i \omega t}e^{-i \theta})}{2i} \frac{(e^{i \Delta\omega t}e^{i \Delta\theta} + e^{-i \Delta\omega t}e^{-i \Delta\theta})}{2}$ $= 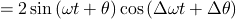2\sin{(\omega t + \theta)}\cos{(\Delta\omega t + \Delta\theta)}$

となる
Δωtが小さいとき、周期Δωtのうなりが生じる

2011/ 6/10